Can a Retail Trader Succeed at Algorithmic Trading? (Part 7)

Today I will conclude with presentation and commentary in an algorithmic trading thread that took place on a popular online forum about 18 months ago.

     > What if you want to make more money; a higher SR? Then you are going
     > to have to move towards (a) the world of HFT and / or (b) the world of
     > weirder, shorter lived alpha-decaying, non linear patterns and/or
     > (c) the world of ‘alternative data’. And away from classical linear
     > statistical methods, towards the wacky world of ML. To play in these
     > worlds you are going to need to make serious investment in automated
     > trading technology, but more importantly you are going to have to be
     > able to use ML properly.
     >
     > The average person using ML in finance does so very badly, and this
     > is based on an observation of ‘professionals’ that doesn’t include the
     > hoards of amateurs who’ve just downloaded a python package and have
     > no idea what they are doing. It’s much easier to overfit with fancy…

Notice the implication here that he has been in position to observe professionals work the craft (of ML). Few can say we have done this. He claims to be an industry professional and I think his writing is very polished. He’s also a book author.

     > ML techniques than with classical ones. Given how much overfitting
     > goes on just using old-fashioned grid searches and regressions, it’s
     > no surprise that overfitting is absolutely endemic within the neural
     > network, AI, non-linear classifying crowd.

This is very consistent with what I learned in Datacamp ML courses.

     > You need a team to do this properly, first because of the alpha
     > decay you are going to spend so much time finding new effects you
     > don’t have time to do anything else like actually implement them.
     > Second, because it’s less likely that a single person will have
     > the full range of skills required to test and implement ML based
     > trading strategies. Such people do exist, but they are rare: after
     > all it’s rare enough to find people with the full set of skills
     > to test and implement classical trading strategies.

Here’s yet another call for a team-based approach (also mentioned in Part 1 and Part 5).

     > What does this mean for the individual trader? Simply put, don’t
     > use ML unless you know exactly what you are doing. And stay
     > away from trading arenas where you need to be able to use ML to
     > discover the edges that exist, plus have access to the technology
     > that will allow you to exploit those edges. There are plenty of
     > areas where you can still compete, but you will have to lower your
     > expectations for SR, and thus increase your bankroll or remain
     > as a part time trader.

Is RC right about these claims? I really don’t know. His credentials look good, but those can be phony. Many details seem consistent with comments I’ve heard elsewhere and for me, convergence usually boosts credibility.

Can a Retail Trader Succeed at Algorithmic Trading? (Part 6)

Today I will continue with presentation and commentary in an algorithmic trading thread that took place on a popular online forum about 18 months ago.

I believe flippant replies like the following are of little use with their absolute, elitist, and hollow claims:

     > The basic fact of the matter: if you love problem solving, the market is just
     > an other [sic] puzzle, and you can have as much money as you want.
     >
     > Its [sic] not in the numbers or indicators, its [sic] the edge around which you
     > design the trading system.
     >
     > Running tests won’t give you the edge, spend time finding your edge [sic:
     > comma splice, John Rubadeau].
     >
     > Thats the core of your system, manual or automated [sic, sic, sic].

I often find such replies to be sorely in need of proofreading, too.

In total contrast, I think the following reply sounds very educated and even brilliant in places:

     > So I think it’s possible for pretty much anyone to make money using
     > simple systematic trading strategies. Most of this money comes from
     > being exposed to diversified sources of risk, so no ‘secret sauce’
     > or fancy ML techniques are needed. These strategies will mostly be
     > quite slow in nature, so not HFT. They will be based on sources of
     > risk premia that decay very slowly, if at all. They will not be high
     > Sharpe Ratio, but by diversifying over a large number of uncorrelated
     > instruments and a number of different strategies I think an expected
     > SR of 1.0 is feasible.

Based on my limited research, I don’t know if I agree with this. I’ve looked at roughly 300 simple strategies on three different markets and none came close to passing the KD criteria although I do believe these criteria to be stringent (probably requiring better than SR of 1.0). Could I trade some of these markets during uncorrelated times (I don’t think it makes as much sense to speak of “uncorrelated markets” because correlation changes) and get an overall SR of 1.0? I would regard this as pretty good because my testing shows SR for the S&P 500 to be around 0.35.

     > Does this count as success? A SR of 1.0 achieved over ten years or
     > more would be top quartile for nearly every hedge fund category.
     > But you will struggle to make a living as a trader with a SR of 1.0,
     > if trading is your only source of income, unless you are very
     > well-capitalized (equates to lower risk and return target).

This is very interesting and theoretical. I would need to backtest and try and correlate SR with annualized return, drawdown, and then figure out reasonable position sizing to determine whether profits could exceed annual living expenses.

I will conclude next time.

Can a Retail Trader Succeed at Algorithmic Trading? (Part 5)

I have been presenting and discussing a thread regarding algorithmic trading that took place in a popular online forum about 18 months ago.

I left off with a reply that concludes:

     > We live in a time where funding is not extremely difficult. From instant loans to
     > credit cards to friends and family to mortgages — if you have an extremely good
     > algo then you’ll get the funds. If you cannot get the funds then you’re probably
     > not smart enough to participate in the industry anyway. Consider it a test.

This reply included some really good points until now when some credibility is lost. I think fundraising is extremely difficult. Then again: 1. I have yet to generate an “extremely good algo” and; 2. maybe I am not smart enough (see third paragraph here about nothing unique) to participate in the industry.

     > As KD said: fitting a strategy to past data is the biggest “crime” I see developers
     > making. But every strategy is dependent on past data at the very least for pattern
     > recognition. When we say a strategy doesn’t “work” anymore, what we’re really
     > saying is that we can’t wait around 50-100 years for it to work again. Because it
     > probably will work again given enough time.

Five stars for this reply, baby! Countless times have I heard/read people say that trading systems break never to be profitable again. One reason for this could be because more and more people trade them, which can kill the edge. As time passes, the number of available strategies approaches infinity faster than the number of traders, which suggests a decreasing likelihood that a particular strategy will be traded live. I therefore believe that strategies no longer in vogue can be profitable again years after their trading frequency diminishes.

Incidentally, this reminds me of the Callan Periodic Table of Investment Returns where we frequently see asset classes that significantly underperform in previous year(s) suddenly start to outperform going forward (the cycle may repeat).

     > De Prado’s point is that since all strategies have a shelf life, you need a team to
     > build a strategy factory for true long term success. He is also not talking about
     > retail but about other’s people money. You can’t take the risk free or index rate
     > for 2 years with OPM while you figure out a new winning strategy without going
     > out of business. A single retail trader could do exactly that.

This is interesting rationale for a team-based approach to trading strategy development. For this and other reasons, I agree with the approach (also discussed in Part 1).

Use of the term “strategy factory” is notable here, too.

I will continue next time.

Can a Retail Trader Succeed at Algorithmic Trading? (Part 4)

Today I continue presentation and commentary on an internet thread (subtitled “KD vs. EC”) regarding algorithmic trading that took place about 18 months ago.

     > I think they are both “right” in their own way. If you look at what KD does,
     > it’s a little different from EC’s strategies.

KD gets his customers to work for him (see second paragraph here)! I wonder how many are aware of this fact.

     > The “trading robots” you see on sites like collective2 aren’t serious edges.
     > Only an idiot would sell a serious proven edge to random Internet anons for
     > pennies on the dollar, and idiots don’t develop profitable trading algos.
     > If you have a proven edge, you raise capital to trade it yourself or sell
     > it to a quant fund for serious lump-sum cash and a job.

As I discussed near the end of Part 3, it’s not so easy to just “raise capital to trade it yourself or sell it to a quant fund.” Proving the edge probably means creating an incubator fund (or friends and family fund, if one can be lucky enough to gather a reasonable minimum amount of capital this way) for purposes of trading and auditing. That can cost many thousands of dollars, which singularly establishes a high barrier to entry.

     > Both of them are nice guys, and I’ve complimented them for their contributions,
     > but neither one of them is really “killing it” in this game. I tend to learn a lot
     > more from those with serious (1M+) skin in the game, and I don’t mean OPM.

We don’t know whether either is “killing it,” much less how much “skin in the game” (actual capital deployed) either has (see fourth paragraph here).

     > And there lies the bait. Yes, in theory a large account can withstand large
     > drawdown if low leverage is used, but most people do not have large accounts,
     > and those that do, will pull the plug if drawdown gets to 20 percent or more.
     > I have seen clients closing accounts after 10 percent loss.

This max drawdown is consistent with the kind of performance I have come to believe is necessary to have something of institutional quality.

     > The algorithms the largest banks and funds use depend on infrastructure or size.
     > There’s almost no way an at-home type trader can participate in this. Many
     > markets have large capital requirements — 100s on millions just to enter.
     > For others you need best co-location or contacts in the industry.

I would imagine these algos are of the HFT variety. I don’t know whether this person knows from experience or is just hypothesizing, but s/he makes some really good logical points. The post continues:

     > I’ve been following people who sell signals for a long time. There are very rarely
     > profitable systems but they always go private fast because selling something that
     > can make millions for thousands is not a business. On top of that you have people

Speaking of someone who has been following signal sellers for a long time, I’d like to hear Mark Hulbert’s take on this.

I will continue next time.

Can a Retail Trader Succeed at Algorithmic Trading? (Part 3)

Today I continue presentation and commentary on an algo trading thread that took place about 18 months ago.

     > Ok, wait a minute: every time traders are talking about big players and market
     > manipulation, everyone seems to agree that algos are running the game. So,
     > assuming that this is right – someone stating that 85% of market is driven by
     > them – that means the big banks, players, etc. actually have financial
     > algorithms that work and are profitable.
     >
     > If this is true, why is there, after decades of banks using them, no market for
     > retail traders to buy them, even if it is not the best/newest version of all?!

This is a very interesting point. Question the premise, though: who is to say that many big firms don’t have profitable algos?

Aside from banks, the “etc.” is probably asset managers and hedge funds. With regard to the former, passage of the Dodd-Frank Wall Street Reform and Consumer Protection Act (July 2010) made it illegal for deposit-taking institutions to engage in prop[rietary] trading. That would include banks and many asset managers. With regard to hedge funds, I studied 2008 – 2016 and found them to underperform (see table here). This may leave some smaller firms that attempt prop trading for a period only to realize they can’t make [enough] money at it and quit. I therefore think it likely that the overall universe for prop trading, where algos are being used to generate the huge Wall Street profits of legend, is significantly diminished.

I’m not convinced that “everyone” (who “seems to agree that algos are running the game”) is all that informed—especially in the face of the kind of reasonable doubt just discussed. People repeat what the financial media writes or broadcasts. Does anyone actually check and scrutinize sources or underlying motives? Not nearly enough, I suspect.

One person responded:

     > The reason is only bank and large firms’ algos can work for them such as
     > market making and HFT. Hardware barrier of entry is in 10s of millions.

I can’t verify the claim of eight figures, but I do believe in a large and formidable barrier to entry.

     > What you are looking for is a strategy can can be deployed on retail
     > level. While those exist, no one in their right mind would disclose it.

This would imply the strategies given by KD (see second-to-last paragraph here) are bogus.

     > It is not that difficult to raise funds and trade it, as long as it
     > indeed has positive expectancy.
     >
     > You will not find it anywhere in public domain.

I don’t believe it is ever easy to raise funds for investment. This article claims the financial services industry has a 12% success rate. Another article claims 90% of financial advisors will fail within the first three years. Claims like these along with the personal roadblocks I have discovered around the wealth management industry make me believe raising money is anything but “easy”—a word that I as a marathon runner will never take for granted (injuries!).

And once again: forget the public domain. You will have to uncover it yourself.

I will continue next time.

Can a Retail Trader Succeed at Algorithmic Trading? (Part 2)

Today I continue presentation and commentary on an internet thread regarding algorithmic trading that took place about 18 months ago.

     > …financial machine learning (ML) is virtually impossible to do right because of the
     > large amount of data you need, awareness of bar types and binning, and many
     > other seemingly trivial but hugely important things. To me, it’s borderline
     > worthless to even try… Leave ML to the MMs and big desks.

I took several Datacamp courses on ML but have yet to do any work of my own in this area. That aside, this sounds like an argument with some teeth.

Someone else commented:

     > BTW, I am disappointed with KD as he doesn’t seem to contribute to the forum.

I couldn’t disagree more. One of my biggest pet peeves is a vendor who shows up online to defend themselves anytime someone writes something that even hints toward negativity (KK is the worst). Do they think they save face by trying to discredit everyone who doesn’t portray them in a brilliant light? While I am skeptical toward reviews and testimonials (see here and third paragraph here), I would sometimes rather let these speak for vendors than the vendors themselves.

This strikes me as one of the best comments of the entire thread:

      • Finding a decision rule with positive expectancy (FDRPE) is… [almost] trivial.
      • FDRPE on daily data that goes back 20+ years is (IMO) foolhardy.
      • FDRPE on daily data that may be tweaked every 6-9-12 months to continue that
         positive outcome… may benefit from [ML] pattern-recognition routines… but…
      • ML depends on data stability that is at odds with the very nature of time-series
         phenomena…

To me, this argues for just how difficult trading strategy development really is (see fourth paragraph here).

     > In my tick-scalping days, I put T/A up that looked good for 20-30 minutes; I relied
     > on it for the next minute or two. For trend-exploitation, I put up daily candles
     > that go back maybe 6-12 months, and rely upon it for the next week or so.

This is shocking, but consistent with my own studies. As discussed in the last three paragraphs here, I did not succeed in looking at four years IS followed by four years OOS and then testing on a subsequent four years. Maybe I should just test the first few trades of OOS2 to see if any edge exists.

Another post reads:

     > You are new here, so I will give you some benefit of the doubt. Get it in your head,
     > you cannot find algo with positive expectancy ANYWHERE. The only way to get it is
     > to create it yourself.

KD disagrees. In fact, if you purchase his product then he gives you several strategies that he says still work in addition to his entire strategy development methodology (don’t mistake this for an endorsement).

I will continue next time.

Can a Retail Trader Succeed at Algorithmic Trading? (Part 1)

I recently stumbled upon a thread on a prominent online forum that is roughly 18 months old. I started reading and realized I have some unique perspectives to share since I am actually ankle-deep in algo trading myself and have taken one of the courses discussed (see second-to-last paragraph here).

The reason I am responding here rather than in the forum itself is because the walls have ears. Internet forums and social media are primary vehicles for communication between retail traders, but vendors often frequent these sites as well. On multiple occasions, I have seen someone subscribed to a trading service get banned by the vendor for posting negative feedback in forums and social media. More details would probably be needed to determine whether this is legal (i.e. do they just get cut off once the subscription runs out? Are they banned immediately with pro rata reimbursement for what subscription remains?), but bottom line is that it happens.

Since I have been a customer—and a customer who does not like to burn bridges—I am keeping personal comments to my unmonetized, low-traffic blog rather than posting in the middle of Grand Central Station.

The thread begins:

     > KD, an (apparently) successful algorithmic trader/author claims simple strategy
     > works and will always work.
     >
     > EC, another guru in this field, however, says simple quant strategies don’t work
     > anymore and machine learning is a must if you want to succeed in trading. He also
     > says that it is impossible to do ML-based system trading on your own; you need a
     > team based approach, since it is so [labor] intensive…

Although I only tested ~300 simple strategies the KD way, none came close to working. Yes, he does teach the simpler the better, and the strategies he gives you as part of his course are simple themselves. Because I couldn’t find anything that met his criteria, though, I have to remain skeptical.

I like the EC comment about doing ML-based strategy development with other people. For multiple reasons, I totally believe trading strategy development should be done in groups (see last paragraph here).

The post continues:

     > I believe EC has gone on record saying the strategies in his book are old strategies
     > that don’t work for him anymore. I wouldn’t be surprised if KD did the same in his
     > book. Seems kind of silly to put strategies in your book you are still using. Both…

Right?! The post continues:

     > publications… are seminal works in retail algo trading. KD is one of the few people
     > with a verifiable record in a trading competition (though we sort of take his word
     > he did it algorithmically). I’d listen to what he has to say…

Interesting comments about KD’s credibility. Yes he was probably verifiable at one point. Is he now? We really don’t know. I’ve been writing on this topic going back many years.

I will continue next time.

General Theories on System Development (Appendix)

In January, I did a two–part blog post with this same title. I also had some additional notes that got saved into a draft and were never published. These additional notes follow for organizational purposes and in the longshot case that someone out there could possibly benefit from any of this (originally from Dec 2012).

———————————-

I make this claim because some people do believe certain characteristics apply to one ticker and not another.  If the tickers are indices then it should be more robust since these are averages of many tickers.

At this point in my young system development career, I’m just not convinced about patterns applying to one ticker and not another.  I really want in the case then certainly they should be able to apply to one index and not another–and it should… If I’m not convinced about the pattern then I should evaluate long and short trades together and if performance is not satisfactory then it’s time to junk this system and move onto the next one. [1]

Furthermore, the more conditions I have to add to a system to get it to backtest well, the less likely it is to perform well in live trading.  This is curve fitting. Since I am so new to system development it might still be worthwhile to go ahead and add additional conditions because only in doing so will I truly develop a feel for the range of performance to be seen.

If I were to add another condition then I would consider a filter to take long (short) trades only when the market is in an uptrend (downtrend).

Alternatively, I could proceed to do maximum adverse (favorable) excursion analysis to see if adding stops and/or profit targets might improve performance.

Should I choose to do neither, then I will table this system for the time being and move onto something else.

Finally, some things to look for when trying to test trading strategies include:

• Long vs. short performance
• Impact of trade delays
• Effect on return-to-risk ratio / max drawdown (reassess subjective function from RRR/MDD to PF + % profitable )

———————————-

Lord help anyone spending a lot of time trying to understand [1]!

Crude Oil Strategy Mining Study (Part 6)

Today I will wrap up with criticism and conclusions from my latest study on crude oil.

Hypothesis[3] is flawed because it contains a future leak. Only in retrospect will I know how the market moves, but the hypothesis must be defined beforehand. Indeed, whether the hypothesis bears out depends on whether the market goes up/down. I clearly have it backwards.

I think the key to avoiding hindsight bias and future leaks is to put myself in the moment of uncertainty and to figure out how I will make the decision. I can easily look back and say “we were in a bull/bear market,” but in the moment all I have are operational definitions that may or may not be effective. Backtesting will determine this.

This is all to say that while the second sentence in paragraph three of Part 4 is easy to say, in the moment I may or may not be able to deliver. In my testing thus far, I have found all lookback periods to face significant challenges.

Perhaps the harshest criticism of this study is that I may have done the statistical analysis incorrectly. I got a #NUM! error in Excel and e-mailed the plug-in developer. His answer—something he admittedly may have failed to mention—made me question the entire battery of tests. The documentation looks tantamount to an entire statistics course. I will review this before analyzing further to make sure I don’t miss anything else. If necessary, I will revisit this post to correct any mistakes.

I didn’t apply the Holm method and I used alpha = 0.05. Hopefully after studying the documentation, I will have a better answer as to whether the former is necessary and/or whether the latter is too high for multiple comparisons.

Turning my final focus to overall conclusions, while many of the differences I presented are statistically significant, they are close to being wrapped around zero. Most performance numbers average out to be slight losers.

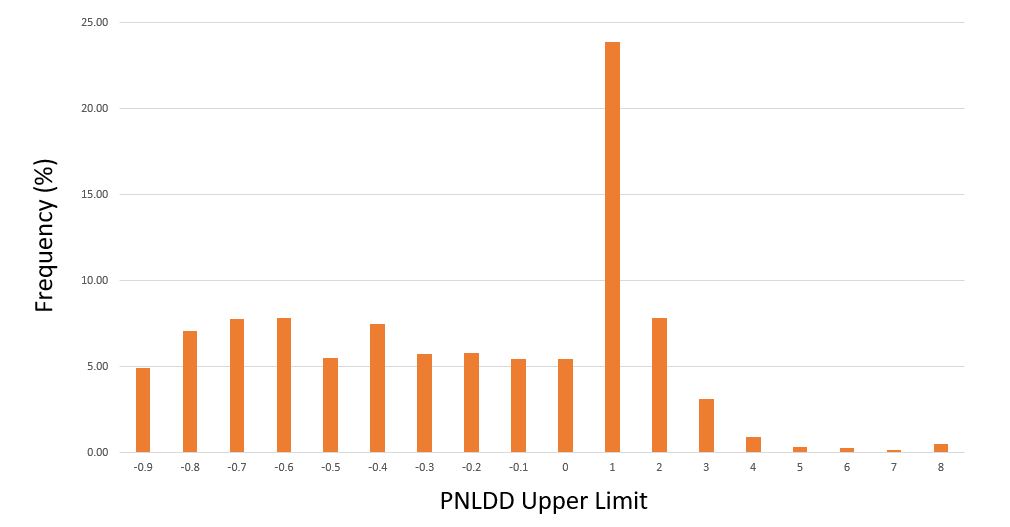
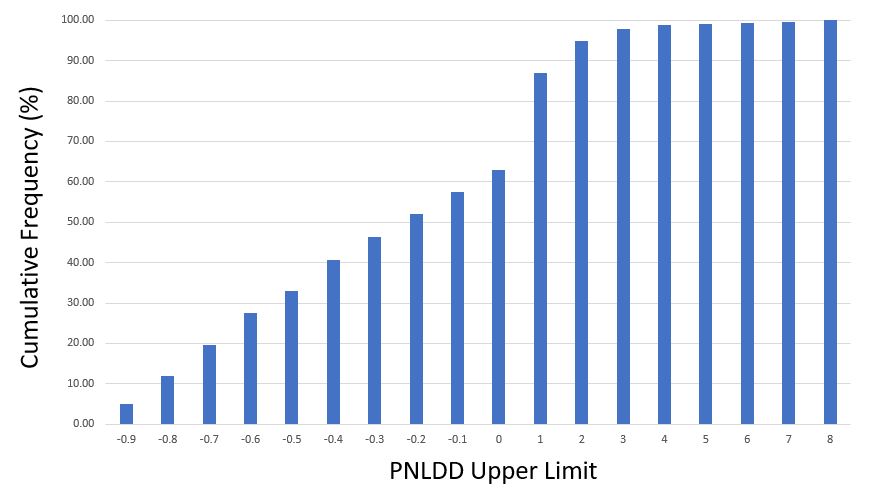
Here are [cumulative] frequency histograms for all 1,632 strategies (i.e. Upper Limit of 1.0 means 0 < PNLDD < 1) :

Strategies clock in with dynamite PNLDD numbers (over 2-3)—but it’s only 5% of the total while other strategies are complete meltdowns (see third-to-last paragraph here). I would discard the horrible ones, but this begs the question how the best strategies generally perform going forward. For the next study, perhaps I will shorten up the time intervals and test an OOS3.

This is only my second mining study, but so far I don’t see a whole lot to be excited about. For me, that does not bode well for algorithmic trading.

Crude Oil Strategy Mining Study (Part 5)

Today I want to continue discussing results from my latest crude oil study.

Monte Carlo drawdown (MC DD) relative to actual DD (fifth-to-last paragraph here) does not seem to be useful. 813 out of 1633 strategies had a MC DD less than the actual DD. These strategies performed significantly worse over incubation than strategies with actual DD less than MC DD (PNLDD -0.11 vs. 0.24, Avg Trade -$59 vs -$15, and PF 0.93 vs. 1.02). While this is somewhat of a surprise, over 81% of these were from the worst group. Best strategies significantly outperformed worst.

Randomized OOS had a significant effect on performance in favor of strategies that pass. In this study, 280 strategies passed Randomized OOS while 1382 failed. Passing strategies averaged 0.13 PNLDD, -$22 Avg Trade, and 0.99 PF versus 0.06, -$40, and 0.97 for failing strategies, respectively.

With regard to worst strategies, none passed Randomized OOS and a vast majority met the MC DD criterion. Best strategies included only a few that passed Randomized OOS and a few that met the MC DD criterion.

Like any study, this study is not without its limitations and/or criticism.

I should have required one Randomized OOS to pass rather than two. On a few occasions, I saw strategies pass and then not pass (or vice versa) upon retest. This made me think the test lacked sensitivity. Because I did not study this over a large sample size, I don’t know how often it actually takes place. In case this makes anybody uncomfortable, one software suggestion would be to make number of Randomized OOS simulations a customizable setting. I would prefer 2,000 simulations to running the test twice in hopes of saving time, but 2,000 curves on the spaghetti graph might be too messy.

I should have programmed the spreadsheet to compute Avg Trade since I recorded Net PNL and number of trades. Automating this would save time and decrease the probability of transcription errors.

I will continue next time.